GED Math Study Guide: Geometry
Geometry is the the study of shapes, space, and measurement. In this section, you’ll explore how to work with lines, angles, and figures, applying rules and formulas to solve real-world problems. Geometry helps you make sense of the physical world, from measuring areas and volumes to understanding how objects fit together. Topics include:
- Perimeter, Area, & Complex Polygons
- Volume & Surface Area
- The Pythagorean Theorem
Perimeter, Area, & Complex Polygons
Perimeter
The perimeter of a two-dimensional shape is the total distance around the shape. To find the perimeter, add up all the sides of a shape. Different shapes have different formulas for perimeter. You need to calculate the perimeter when building fences, framing pictures, or measuring the outline of a given space.
Note
Sometimes, the question may offer shapes with missing side lengths. Look for right angles, parallel sides, or given relationships that let you deduce unknown sides.
Perimeters of Common Shapes
| Shape | Formula | Variables |
| Square | \(P = 4s\) | \(s =\) side length |
| Rectangle | \(P = 2 (l + w)\) | \(l\) = length, \(w\) = width |
| Triangle | \(P = a + b + c\) | \(a, b, c\) = side lengths |
| Circle | \(C = 2 \pi r\) | \(C\) = circumference, \(r\) = radius |
Area
Area measures how much space a two-dimensional shape covers. You need to calculate area when dealing with scenarios like figuring out how much paint you need for a wall or how much carpet will cover a floor.
Areas of Common Shapes
| Shape | Formula | Variables |
| Square | \(A = s^2\) | \(s\) = side length |
| Rectangle | \(A = l \times w\) | \(l\) = length, \(w\) = width |
| Triangle | \(A = \dfrac{1}{2} \times b \times h\) | \(b\) = base, \(h\) = height |
| Circle | \(A = \pi r^2\) | \(r\) = radius |
Complex Polygons
To find the area of a complex polygon, split the polygon into its component rectangles and shapes. For example, the complex polygon below can be split into two shapes.

The area of the complex polygon = Area of Rectangle A + Area of Square B

Volume & Surface Area
Volume
The volume of a three-dimensional shape tells us how much space it occupies or how much it can hold inside. Different shapes, like cubes, cylinders, and pyramids, each have their own formula for calculating volume. Understanding these formulas helps us solve real-world problems involving containers, buildings, and 3D objects. By measuring length, width, and height, we can determine exactly how much material or space we’re working with.
Volumes of common shapes
| Shape | Formula | Variables |
| Cube | \(V = s^3\) | \(s\) = side length |
| Rectangular Prism | \(V = l \times w \times h\) | \(l\) = length, \(w\) = width, \(h\) = height |
| Cylinder | \(V = \pi r^2h\) | \(r\) = radius, \(h\) = height |
| Sphere | \(V = \left(\dfrac{4}{3}\right) \pi r^3\) | \(r\) = radius |
| Cone | \(V = \left(\dfrac{1}{3}\right) \pi r^2h\) | \(r\) = radius, \(h\) = height |
| Pyramid | \(V = \left(\dfrac{1}{3}\right)Bh\) | \(B\) = base area, \(h\) = height |
Surface Area
The surface area of a three-dimensional shape measures the total area of all its exterior faces or surfaces. By finding the surface area, we can calculate costs for covering three-dimensional objects, such as when painting, wrapping packages, or determining material needs for construction.
| Shape | Surface Area Formula | Variables |
| Cube | \(SA = 6s^2\) | \(s\) = side length |
| Rectangular Prism | \(SA = 2(lw + lh + wh)\) | \(l\) = length, \(w\) = width, \(h\) = height |
| Cylinder | \(SA = 2 \pi r^2 + 2 \pi rh\) | \(r\) = radius, \(h\) = height |
| Sphere | \(SA = 4 \pi r^2\) | \(r\) = radius |
| Cone | \(SA = \pi r^2 + \pi rl\) | \(r\) = radius, \(l\) = slant height |
| Pyramid | \(SA = B + (1/2)Pl\) | \(B\) = base area, \(P\) = base perimeter, \(l\) = slant height |
The Pythagorean Theorem
The Pythagorean Theorem states that, in a right triangle, the square of the hypotenuse equals the sum of squares of the other two sides (e.g., the legs).
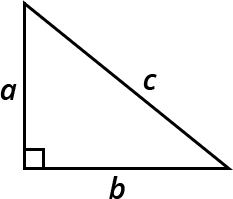
It is written as \(a^2 + b^2 = c^2\). The legs of a triangle are the two sides that form the right angle, while the hypotenuse is the longest side, or the side across from the right angle. The theorem can be applied whenever we encounter right angles in the physical world. By knowing just two sides of a right triangle, we can always find the third. It helps us solve practical problems in construction, navigation, and design.
After reviewing all the material above, take the geometry review quiz below to check your understanding. The questions will cover every major topic in this section, and you can use the official GED formula sheet at any time as a reference. This is your chance to put everything you’ve learned into practice!
