GED Math Study Guide: Basic Math
Welcome to the fundamental building blocks of mathematics! This section covers the essential math skills you’ll need to master for the GED test and beyond, taking you step by step through the following topics:
- Number Sense
- Factors & Multiples
- Fractions, Decimals, & Percents
- Ratios, Proportions, Rates, & Scaling
Number Sense
Number sense is your mathematical foundation. Understanding different types of numbers, how to work with them accurately, and how they relate to each other on the number line will give you the confidence to tackle any math problem that comes your way.
Essential Number Concepts
Integers: All whole numbers (positive, negative, and zero).
Examples: \(…−3, −2, −1, 0, 1, 2, 3…\)
Rational Numbers: Numbers that can be written as a fraction \(\frac{p}{q}\), where \(p\) and \(q\) are integers and \(q≠0\).
All integers are also rational numbers (e.g., \(5 = \frac{5}{1}\) ).
Rounding
In a whole number, each digit has a place (ones, tens, hundreds, thousands, etc).
In decimals (e.g., 45.678), digits to the right of the decimal represent tenths, hundredths, thousandths, etc.
When performing rounding operations, first identify the digit to round. It will be mentioned in the question. Then, look at the digit immediately to the right:
- If it is 0, 1, 2, 3, or 4, round down (keep the rounding digit the same).
- If it is 5, 6, 7, 8, or 9, round up (add 1 to the rounding digit).
Example 1:
Round 456 to the nearest tens place:
The tens place is 5. The next digit (in the ones place) is 6.
Since the ones digit (6) is 5 or more, round up.
456 becomes 460.
Example 2:
Round 3.14283 to the nearest hundredths:
The hundredths digit is 4. The next digit (thousandths) is 2.
Since \(2 \lt 5\), round down (keep the 4 as is).
3.14283 becomes 3.14.
Example 3:
Round 5.291 to the nearest tenths:
The tenths digit is 2. The next digit (hundredths) is 9.
Since \(9 \gt 2\), round up (add 1 to 2).
5.291 becomes 5.3.
Note
Rounding can help you check if an answer is in the right ballpark. For instance, if you need to multiply \(197 \times 4\), you can round 197 to the nearest hundred (200) and then calculate \( 200 \times 4 = 800\).
The Number Line & Absolute Value
A number line is a visual tool that represents numbers in order from least (to the left) to greatest (to the right).

Negative numbers are to the left of 0 (−1, −2, −3, …).
Positive numbers are to the right of 0 (1, 2, 3, …).
0 is neither positive nor negative.
Distance on the number line:
The absolute value of a number \(n\), written as \(∣n∣\), is its distance from 0 on the number line (It is always non-negative).
- \(\lvert 5 \rvert = 5\) because \(5\) is five units to the right of 0.
- \(\lvert −3 \rvert = 3\) because \(−3\) is three units to the left of 0, so the distance is a positive 3.
Example:
What is the distance between the points X and Y on the number line?
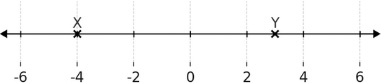
Distance of the point X from 0 is \(\lvert −4 \rvert = 4\).
Distance of the point Y from 0 is \(\lvert 3 \rvert = 3\).
Distance between X and Y = \(4 + 3 = 7\).
Order of Operations (PEMDAS)
When you see an expression like \(5 + 6 \times 2^2 − (9÷ 3)\), you should follow the PEMDAS rule to determine in which order you do the operations:
- Parentheses (or other grouping symbols like brackets)
- Exponents (including powers and roots)
- Multiplication and Division (from left to right)
- Addition and Subtraction (from left to right)
So,
\(5 + 6 \times 2^2 − (9 ÷ 3)\)
\(5 + 6 \times 2^2 − 3\)
\(5 + 6 \times 4 − 3\)
\(5 + 24 − 3\)
\(29 − 3\)
\(26\)
Factors & Multiples
Factors and multiples are the mathematical tools that help you break numbers down into their building blocks and find common ground between different numbers. These skills will make fraction operations much easier and help you solve real-world problems about grouping, scheduling, and finding patterns.
Greatest Common Factor (GCF)
The Greatest Common Factor (GCF) of two numbers is the largest integer that divides both numbers without leaving a remainder.
How to Find the GCF
Step 1: List all factors of each number.
Step 2: Identify the largest factor common to both lists.
Example: Find the GCF of 12 and 18.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 18: 1, 2, 3, 6, 9, 18
Common factors: 1, 2, 3, 6
The greatest common factor is 6.
Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two numbers is the smallest non-zero number that is a multiple of both.
How to Find the LCM
Step 1: List several multiples of each number.
Step 2: The first common multiple (besides 0) is the LCM.
Example:
Find the LCM of 4 and 6.
Multiples of 4: 4, 8, 12, 16, 20 …
Multiples of 6: 6, 12, 18, 24 …
Common multiples include 12, 24, 36 …
The least of these is 12.
Applications of GCF & LCM
GCF and LCM are used in fraction operations like reducing fractions and adding or subtracting fractions.
GCF also appears in problems about grouping items into the largest possible “equal groups.” LCM often comes up in scheduling or repeating events (e.g., “When will two lights blink together next?”).
Example:
You are packing food donations to go out to local families, and you just received a donation from a local orchard of 24 apples and 30 pears. To divide the fruit into bags of equal size so that each family gets the same amount, find the GCF of 24 and 30.
The GCF of 24 and 30 is 6. Thus, the fruit can go in six bags of equal size, providing six families with four apples and five pears.
Fractions, Decimals, & Percents
Understanding how to work with fractions, decimals, and percents is essential for solving everyday math problems and for success on the GED.
Simplifying Fractions:
To simplify a fraction, divide both the numerator and the denominator by their greatest common factor (GCF).
Example:
\(\dfrac{18}{24} = \dfrac{18 \div 6}{24 \div 6} = \dfrac{3}{4}\) (GCF of 18 and 24 is 6).
Converting Improper Fractions to Mixed Numbers
In an improper fraction, the numerator is greater than its denominator (e.g., \(\frac{7}{4}\)). It can be converted and expressed as a mixed number (a whole number plus a fraction) with the following steps:
Step 1: Divide the numerator by the denominator: \(7 \div 4 \gets 1 \) remainder 3.
Step 2: Write the mixed number as \(1 \frac{3}{4}\).
Operations with Fractions
For adding and subtracting fractions, find a common denominator and convert each fraction to an equivalent fraction with that common denominator.
Example:
\(\dfrac{1}{3} + \dfrac{2}{5} = \dfrac{5}{15} + \dfrac{6}{15} = \dfrac{11}{15}\)
For multiplying fractions, multiply their numerators together and the denominators together.
Example:
\(\dfrac{1}{3} \times \dfrac{2}{5} = \dfrac{1 \times 2}{3 \times 5} = \dfrac{2}{15}\)
To divide two fractions, multiply the first fraction by the reciprocal of the second fraction.
Example:
\(\dfrac{1}{3} \div \dfrac{2}{5} = \dfrac{1}{3} \times \dfrac{5}{2} = \dfrac{5}{6}\)
Operations with Decimals
For adding and subtracting decimals, align decimal points vertically, then add or subtract as with whole numbers.
For multiplying decimals, multiply them as whole numbers and then place the decimal point in the product according to the total number of digits to the right of both decimals.
Example: \(3.2 \times 0.5\)
Multiply as whole numbers (\(32 \times 5 = 160\)) and then move the decimal two places.
\(3.2 \times 0.5 = 1.6\)
For division, move the decimal in the divisor to make the divisor a whole number (and move the dividend the same number of places), then divide normally.
Example: \(3.2 \div 0.5 = 32 \div 5 = 6.4\)
For conversions between fractions, decimals, and percentages:
Fraction → Percent: Convert the fraction to a decimal, then multiply by 100 and add “%.”
Example: \(\dfrac{3}{4} = 0.75 = 75\%\)
Decimal → Percent: Multiply by 100 and add “%.”
Example: \(0.22 = 22\%\)
Percent → Decimal: Divide by 100.
Example: \(45\% = \dfrac{45}{100} = 0.45\)
Calculating Percent Increase/Decrease
To find the percent increase or decrease between two values, first find the difference between the two values. Then, divide the difference by the original value and multiply by a hundred to convert to a percentage.
Example: A product’s price goes from $50 to $60.
Percentage increase:
\(= \dfrac{\text{difference in values}}{\text{original value}} \times 100 \)
\( = \dfrac{60-50}{50} \times 100 = 20\%\)
Weighted Percentage
A weighted percentage is used when different parts of a total have different levels of importance. Instead of averaging all parts equally, each part is multiplied by its assigned weight (how much it counts toward the final result). Then, you add those weighted parts together to get one overall percentage.
Example
There are 2 tests in a course. The marks scored in test 1 count for 40% of the final grade, and the marks scored in test 2 count for 60% of the final grade. If a student scores 90% on test 1 and 80% on test 2, what is the final grade percentage?
Final Weighted Grade Percentage
\(= (90\% \times 0.40) + (80\% \times 0.60)\)
\(= 36\% + 48\% = 84\%\)
Ratios, Proportions, Rates, & Scaling Factor
This section will help you solve real-world problems by showing how quantities relate to each other through ratios, proportions, rates, and scale.
Ratios, Proportions, and Rates
A ratio compares two quantities with a shared characteristic. You can express a ratio as a fraction \(\left(\frac{a}{b}\right)\) or using a colon \((a:b)\).
Example: If you have 6 apples and 3 oranges, the ratio of apples to oranges is \(\frac{6}{3} = 2,\) or \(6:3\), which simplifies to \(2:1\).
To simplify (reduce) a ratio, divide both parts by their greatest common factor (GCF).
Example: \(8:4\) simplifies to \(2:1\) (because the GCF of 8 and 4 is 4).
A proportion is a statement that two ratios are equal:
\(\dfrac{a}{b} = \dfrac{c}{d}\)
This implies \(a:b\) is proportional to \(c:d\).
Note
Proportions are common in recipes, maps, scale models, and other scenarios where one ratio must remain consistent with another.
A rate is a special kind of ratio comparing quantities with different units. For example:
- Miles per hour (distance vs. time)
- Cost per pound (price vs. weight)
- Dollars per hour (wages vs. time)
Example: If a car travels 150 miles in 3 hours, its rate (speed) is:
\(\dfrac{150 \text{ miles}}{3 \text{ hours}} = 50 \text{ miles per hour}\)
Questions involving rates are usually word problems about speed (distance/time), unit price (total cost/quantity), and hourly wage (total pay/hours worked).
Scaling Factor in Measurement
A scaling factor tells you how much the length in a diagram or model is enlarged or reduced relative to the real-life object. This is not about converting units like inches to centimeters; rather, it’s about maintaining a consistent ratio between a representation and actual size.
For example, if 1 inch on a blueprint equals 10 feet in real life, we treat that as a consistent ratio (scale factor). A model of a building might have a 1:50 scale, meaning 1 unit in the model corresponds to 50 of the same units in reality.
Example: A scale model of a car is at 1:20 (1 model unit for every 20 real units). If the model car’s length is 6 inches, the real car’s length is \(6 \times 20 = 120\) inches.
Basic Exponents & Radicals
Basic Exponent Rules
Product of Like Bases: Keep the same base and add exponents.
\(2^3 \times 2^2 = 2^5 = 32\)
Quotient of Like Bases: Keep the same base and subtract exponents.
\(2^5 \div 2^2 =2^{5-2} = 2^3 = 8 \)
Power of a Power: Multiply the exponents.
\((3^2)^3 = 3^{2 \times 3} = 3^6 = 729\)
Zero Exponent: any number raised to the power of 0 will result in 1.
\(5^0 = 1\)
Roots & Radicals
The square root of a number \(x\), written as \(\sqrt{x}\), is the number that, when multiplied by itself, equals \(x\).
Example: \(\sqrt{25} = 5\) because \(5 \times 5 = 25\).
A perfect square is an integer that is the square of another integer.
Examples: \(1 = 1^2, 4 = 2^2, 9 = 3^2\) and so on.
You can break down a square root using factorization.
Example: \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{5 \times 5 \times 2} = 5 \times \sqrt{2}\)
\(\sqrt{x} \) is the same as \(x^{\frac{1}{2}}\).
Example: \(\sqrt{16} =(16)^{\frac{1}{2}} = 4 \)
Now that you have reviewed the foundation of math, take our basic math review quiz below to check your understanding. Then, once you’ve mastered this section, move on to the algebra section of our study guide to build on your math skills.
